My linchpin is the “Rules” for Order of Operations. Students must follow the rules to the order of mathematical operations in order to come to the same conclusion as the mathematical world set forth.
My evidence is student work. I gave a pretest that showed the students knew more than I expected. It was too easy and pointless to give it as a post-test. I will make this modification in my lesson plan to make a test that has more challenging problems. After their first book assignment I modified my unit to a higher level (Algebra). The unit was limited to simple grouping symbols and so I added solving expressions through substitution that used exponents and grouping symbols.
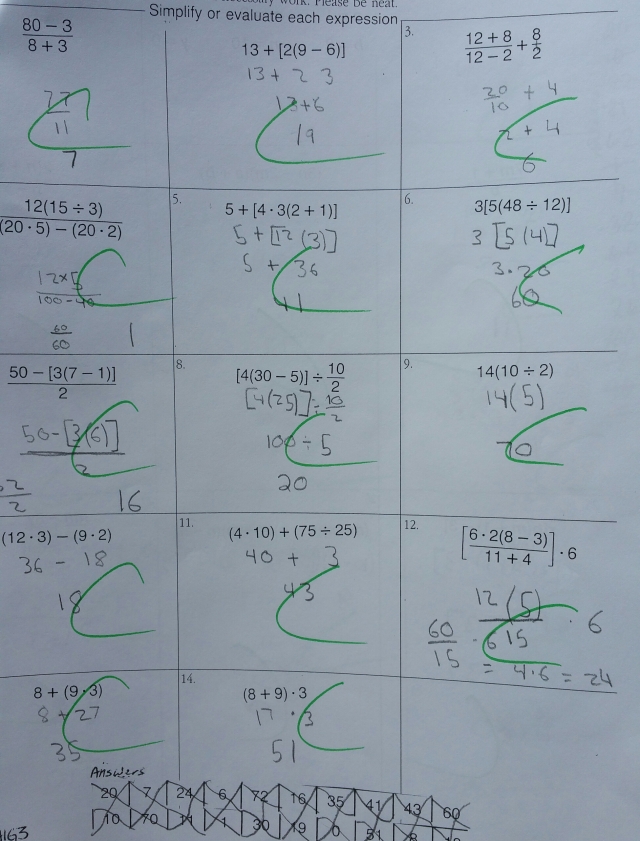
This is the assignment out of their book. You can see the Pre-algebra is a pretty simple “Order of Operations”. This is a typical result of the students’ work from this assignment. It was the first assignment of the unit after the pre-test. The red check marks are made when the student graded their paper. I also corrected the paper and made the green marks. I want the students to see how they did and I wanted to know how they did. I also pay attention to how they grade their paper. Are they doing it correctly or not. This helps me understand the student better.
At this is when I decided that I needed to take the students to a higher level to challenge them. The most incorrect on this assignment that was turned in was three problems.
You can see they needed to subtract before they add (marked in green), because addition and subtraction are equivalent operations with an addition rule of left to right when you have more than one. The subtraction is to the left of the addition sign.
The next three assignments were from Pizzazz so they have the answers with a pun joke. It is harder to catch the individual errors to make the corrections. I didn’t like how the students were writing notes around the problem. I did appreciate that they took the time to write down a portion of their answer and not trying to remember everything. These worksheets are great for immediate feedback. The students are trained to look for their answer to make sure they are on track.

The students love these worksheets. They don’t always ask for help when they need it. They just keep trying. I grade these papers too so I can see where they can use assistance with the rules of order.
I realized that I wasn’t getting the full picture of how the students were doing, due to them not writing in the mathematical language. So I switched to creating my own worksheets that provided room to write in the mathematical language. To keep the confidence in the students I provided the answers on the paper where they can be assured of doing the work correctly.
Again, I felt that the students could go a little higher. I decided the answers were now hindering my evaluation of their work. It wasn’t allowing me to see the mistakes that I could discuss with the students.
Up to this point all the students were only missing a problem here or there. Students asked for help when there was an exponent outside the parenthesis and a number in front of the parentheses. For example, 3(4)2, some of the students multiplied 3×4 before using the exponent. I had to show them that the exponent only had the 4 inside and the 3 was a separate entity then the exponent. This was very appropriate for this lesson. The little errors that they are making are different with each student and we need to sort out the errors and correct them. The next time I teach this unit I will be sure to point this out and emphasize that it is a common error that needs to be corrected.
I made the switch to no answer on the worksheets and created a worksheet that gradually move to a higher level of challenge. As a class the students did well on the first six problems and made similar errors on the next set of problems. With the next set of worksheets I did the grading and returned the worksheet back to the students to make corrections. I would use two different color markers to show where the students made their error and a second mark to show if they fixed it or not. My first student that I will follow had made tremendous gains. She took advantage of the individual instructions and corrected the errors.
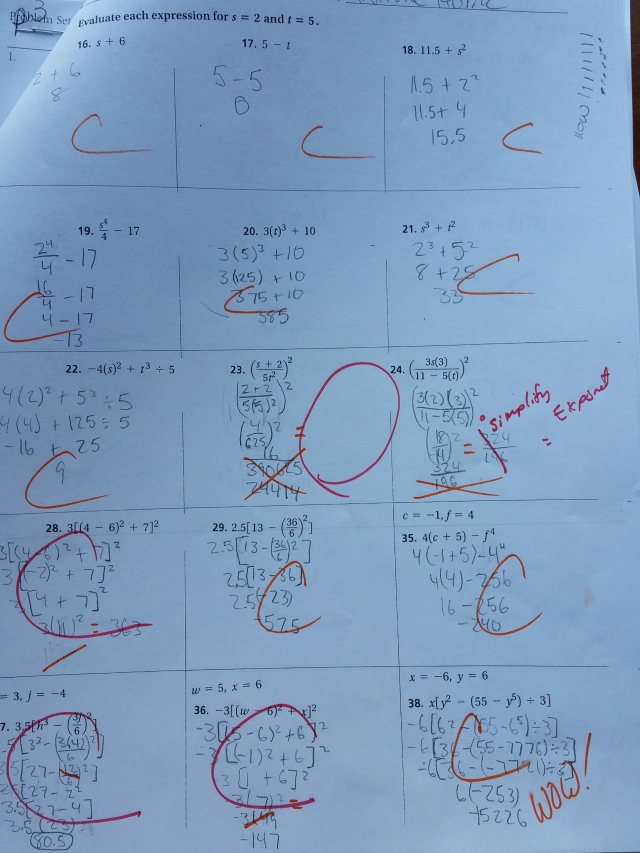
So, here in the picture the first six problems were pretty easy for most of the students.
As we get into the grouping symbols the students weren’t sure what to do with the fractions (#24). After a couple of days of practice and instructions they understood to simplify the fraction before applying the exponent. The students wanted to divide and leave a decimal for an answer. This is an application of learning the fraction bar is a division sign.
This student had shown great growth in her learning. She did a great job writing in the mathematical language, this helped her stay on the right track.
After an assignment I tallied the problems that students were having trouble with. This helped me to see who was having trouble with which problems. I could see how well a student was doing by looking at their graded assignment, but I wanted see which problems were giving them trouble.
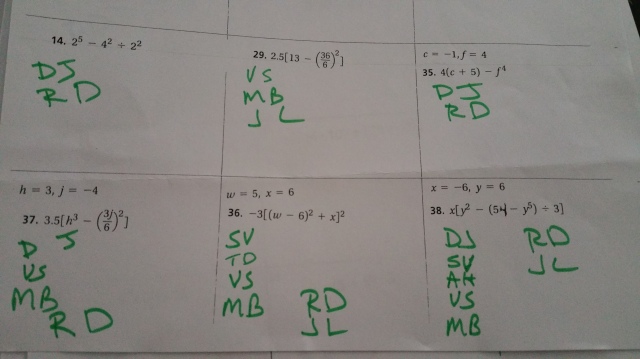
After I finish grading their papers I write their initials by the problem so I know which ones we can focus on.
On the next assignment, I graded and immediately returned their work to them for corrections. The students were happy to see their own progress and that I had pointed out to them the step that they missed.

You can see I graded with blue first and this student had subtracted before dividing. With the mark on the paper she knew she had to divide before subtracting. On the last problem she had to correct she didn’t take care of the parenthesis first.

On the last assignment before our final assessment we focused on simplifying fractions before using the exponents. The two different types confused the students. The first one #11, the fractions can divide down to a 3 and that is cubed and the second one doesn’t come out of the fraction and both numbers have to have the power of 4 applied to it and is left as a fraction.
You can see on her final assessment she was able to do the first one with out assistance. I had graded their paper and either marked it correct or wrong without instructions. The students were allowed to make any corrections they needed to. Most of the students took advantage of this opportunity.
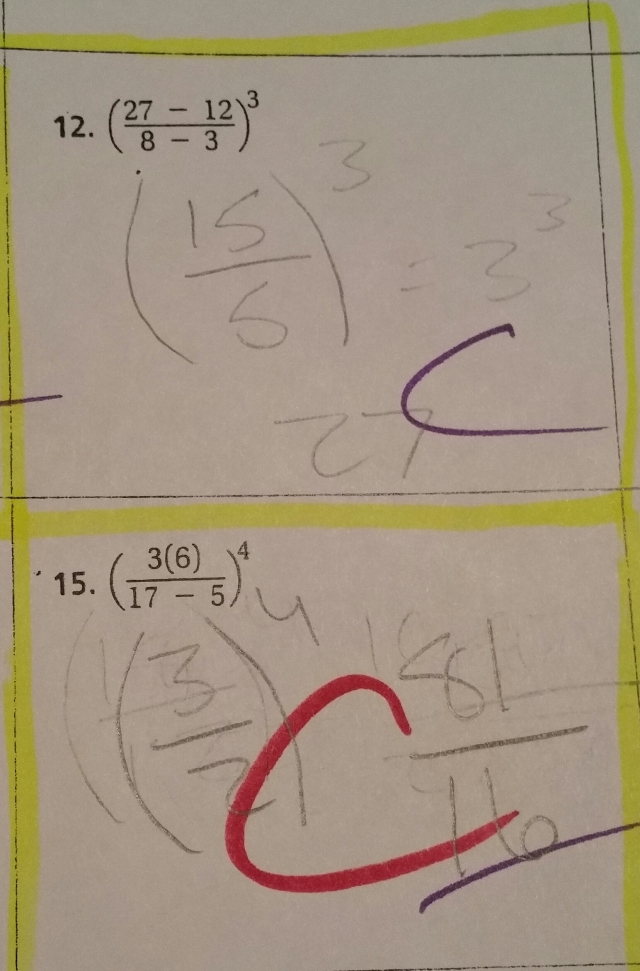
When I had returned the test for corrections I did announce for them to remember to simplify your fractions before using your exponents. Several students understood and made the corrections.
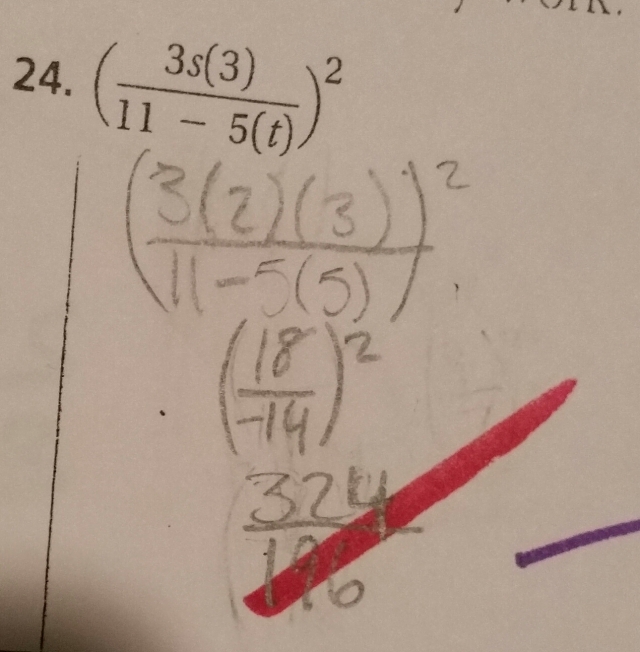
The first student had done exceptionally well on her final assessment. She had only missed one problem and was only able to redo the problem half way through before making an error. She received almost full credit for this work.
When she did her correction she just didn’t simplify her fraction before using the exponent. This is her only error on the final assessment. SUCCESS!
This is the same error as the others. This is an algebra problem and it seems to be the concept that is a bit of a stretch for these students. This reminds me that it is a sign of being in the right place. The students are still challenged and are rising to meet the challenge.
Overall, I am very proud how hard the students worked at conquering this concept. The start of the unit they weren’t writing in the mathematical language and by the end of the unit they were not just writing in the language, but the 80-95% of the answer were correct at the algebra level. They rose above the level expected of them and yet when I raise the standard they almost conquered it. In my lesson plans I will expand the lesson to algebra standards and will emphasize simplifying fractions that don’t divide out. I will have more instruction and practice on switching between the two different types of fractions (one simplifies and the other divides out). The Math Antic videos do a great job with pre-algebra order of operations these videos gave us a great launch into the unit.
In the beginning of the unit I had the students play “Rags to Riches” (Who wants to be a millionaire?) game show where they had to complete Order of Operation problems correctly and try to win a million dollars. The students loved trying to win the money. They worked hard to win and were very proud when they did. One of the girls said she went home and played until she won. This game provided great extra practice. This worked well the first three days then I didn’t have time to create new games to coincide with their work for the next days to come. The assessing their work had taken more time than I expected. Time well spent on analysis so I will slowly add to “Rags to Riches” games at a higher level as I teach this unit next time.
At the first part of the unit the students were in groups to help each other with the problems. I eventually was able to stagger their work where they sat in groups but they were busy making their own corrections which made them work at their own pace. This gave me time to work with each student individually, where I could analyze their work and discuss it with them.
The extent of assessing the data of the students’ work and test is not normally done in my classroom practices. I do this normally with the assessments to see what I need to continue to teach, but to do it with the assignments help to bring more students to a higher level of success. I will have to shorten assignments in my classes to make this possible. I am impressed with the success of the students and I believe they are too. This lesson, with all the modifications, has been very successful.

